General Dynamic Time Warping: Let’s do the time warp again
I had the great fortune of working on a paper with Professor Stephen Boyd at Stanford, where we discuss a method for aligning two time-series together called general dynamic time warping (GDTW).
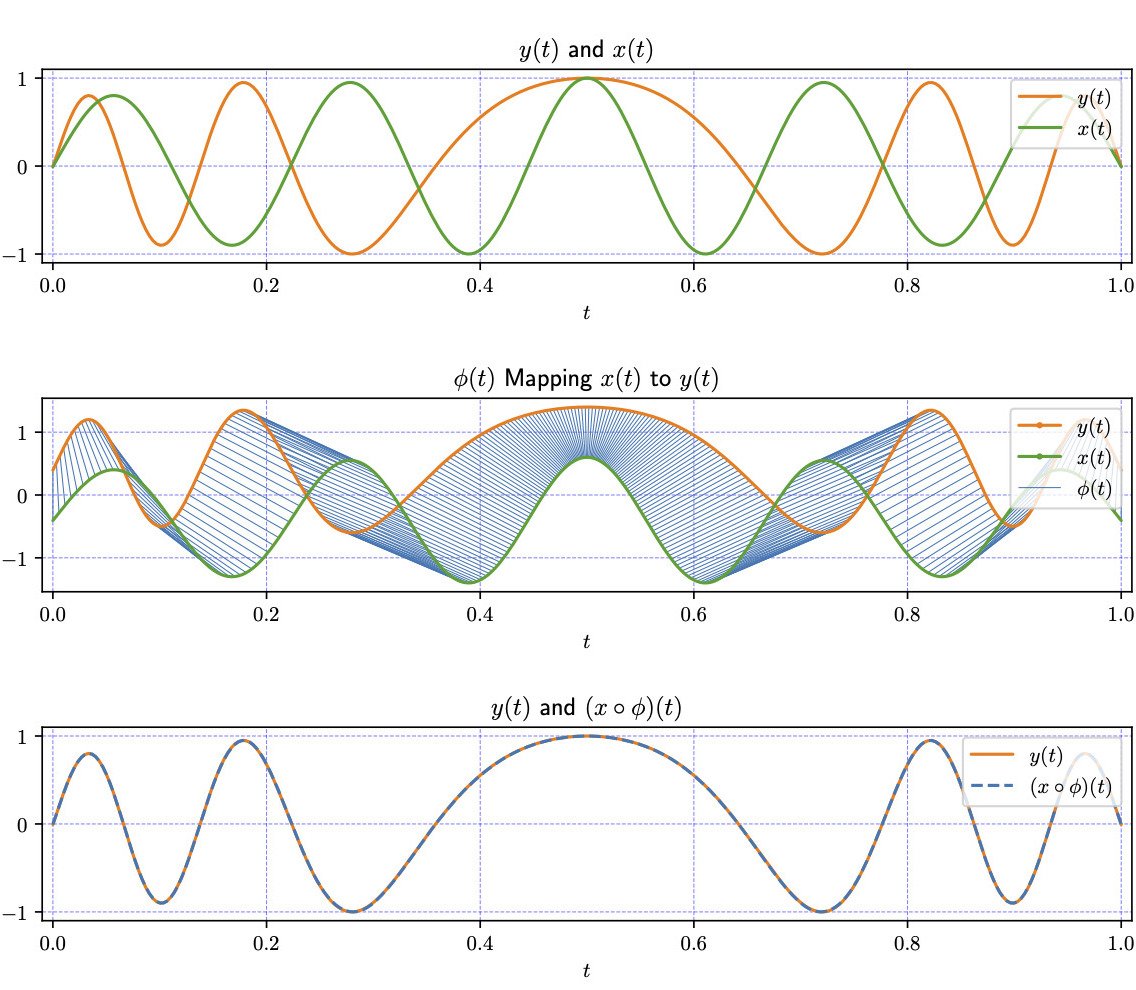
To better understand the problem, consider the example below. The top plot shows two signals that we seek to align. The middle plot shows the mapping between the two signals defined by the time warping function, phi. The bottom plot shows how the two signals look when we compose signal x with the time warping function; it aligns beautifully with y. The approach is powerful, fast, and also works with groups of signals.
To shape the solution, there are two parameters. One adjusts the smoothness of the mapping, and the other tries to create the gentlest mapping possible. To illustrate, there is a live example where you can adjust these in real-time and observe changes in the solution.
I realized this was an important problem when my team and I at Bluue were having trouble aligning time-series data collected from our device. Though we appreciated previous contributions from other researchers, weren't satisfied with existing methods since they had sharp irregularities in the solution that distorted the sensitive bio-potentials. We were shocked that nothing out there could address this common use-case, and so with only a few rough ideas in mind, I asked Professor Boyd for his thoughts. Together we realized it was indeed important, and we worked out a solution.
Professor Boyd offered clarity on the problem itself, which in retrospect was 99% of the hard work. I'll never forget the agility with which he linearized our thinking and writing. There were so many mind-bending lessons I learned in the process of our work together, but if there is any one takeaway that I would share above all, it's this: have "absolute clarity."
Although the math was and algorithm was relatively straightforward discrete optimization and dynamic programming, which I had experience with when deriving the routing system for Caviar, I have to say it was very difficult to get this particular algorithm to work consistently in practice. One of the challenges of iterative refinement is that small numerical errors can become greatly amplified in subsequent steps. Until I was able to root-cause and address the various numerical issues, it would work well but, to my great frustration, would randomly result in a catastrophic failure, e.g. segfault. One of the key insights was to stay well below machine epsilon when checking constraints, e.g. x < (max_val - eps) where eps is something liberal like 1E-10 (see source code). While I think AI can help developers over similar obstacles, I did not have these tools at the time and had to figure this out through patience, perseverance, and coffee. In the end, I built an entire workbench devoted to debugging dynamic programs, which was a thankless, but ultimately necessary development step. However, the workbench proved useful and helped create a whole suite of dynamic-programming based algorithms at Bluue, which I one day hope to publish and open-source.
Although this project was inspired by my work in industry, I want to be clear that it is an academic contribution to the community. Please feel free to use our software in your own projects, even if they are startups. It should hopefully be easy to install with pip gdtw. Also, the code is available on Github under a very liberal Apache license. In fact, if you have an interesting downstream application in mind, please feel free to reach out if you need pointers.
Like the classic Rocky Horror song "let's do the time warp," I hope this method brings you as much joy as it does for me.